 Ci sono volte in cui anche delle semplici strutture a pianta rettangolare nascondono delle insidie che richiedono ulteriori livelli di approfondimento del modello di calcolo strutturale. La mia libera professione è fatta esclusivamente di collaborazioni con progettisti architettonici del cui lavoro curo l’aspetto strutturale garantendo, per quanto possibile dalla tecnica (e dalle normative), di esprimersi quanto più liberamente possibile. In questo esempio voglio condividere con voi lettori un’interessante esperienza frutto di diverse riflessioni.
Ci sono volte in cui anche delle semplici strutture a pianta rettangolare nascondono delle insidie che richiedono ulteriori livelli di approfondimento del modello di calcolo strutturale. La mia libera professione è fatta esclusivamente di collaborazioni con progettisti architettonici del cui lavoro curo l’aspetto strutturale garantendo, per quanto possibile dalla tecnica (e dalle normative), di esprimersi quanto più liberamente possibile. In questo esempio voglio condividere con voi lettori un’interessante esperienza frutto di diverse riflessioni.
Ci occuperemo di un corpo (vedi Figura 1 – Corpo A) di un complesso residenziale a corte, le cui scale e vano ascensore sono collocati al centro della corte stessa e realizzati con giunto tecnico rispetto ai singoli volumi architettonici. Rispetto ad un usuale edificio residenziale l’aspetto strutturalmente positivo è che almeno questi elementi funzionali di collegamento non “impattano” sulla regolarità strutturale. Sappiamo tutti che i nostri modelli di calcolo funzionano perfettamente fin quando non ci preoccupiamo di modellare scale e vani ascensore, i cui elementi rappresentano vere e proprie “concentrazioni di rigidezze” capaci di rendere il comportamento deformabile torsionalmente.
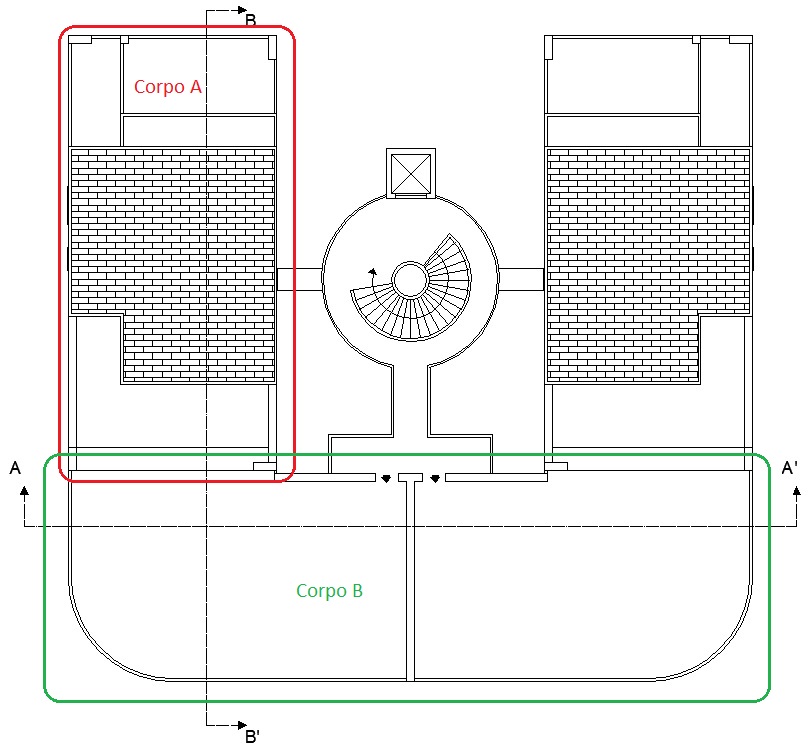
Figura 1: Pianta copertura del complesso
Per i dei due corpi simmetrici posti lungo l’asse Y (di dimensioni 8×16.7 m), le particolarità sono concentrate sia nelle distribuzioni delle tamponature (e delle aperture) sia nella forma dei solai, nei quali sono presenti vuoti e discontinuità diverse ad ogni livello. Nella figura successiva possiamo notare questi aspetti per i vari piani:
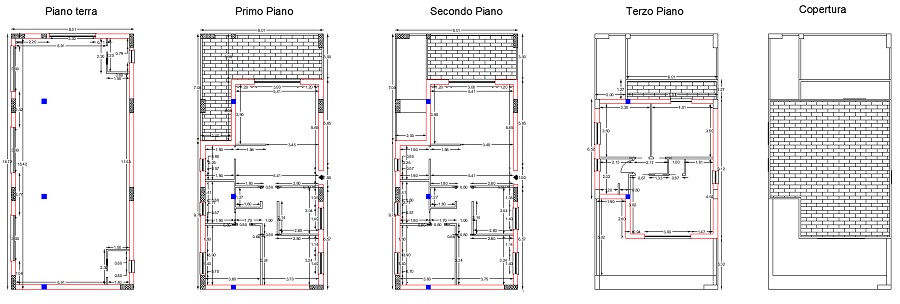
Figura 2: Piante dei vari livelli
Relativamente alla Figura 2 è possibile notare la presenza di alcuni pilastri di colore blu, i quali sono stati oggetto sin da subito di “discussione” (ovviamente amichevole e costruttiva) in quanto non presenti nel progetto originale. Si è concluso con un “patteggiamento”: lasciamo i pilastri ma facciamoli piccoli… La scelta di dimensioni ridotte (30×30 cm) ha condizionato il tipo di progettazione antisismica da effettuare, in quanto la verifica di gerarchia delle resistenze e la duttilità al piede si sono rivelate “insuperabili”.
Nel caso in esame, la bassa accelerazione SLV del sito (circa 0.14 g) ha consentito che tali problemi vengano superati mediante una progettazione di tipo “non dissipativa”, che però ha comportato una maggiore robustezza delle altre colonne e dell’insieme della struttura.
Maggiore chiarezza può essere fatta dalla rappresentazione 3D della costruzione e della struttura (vedi Figura 3):
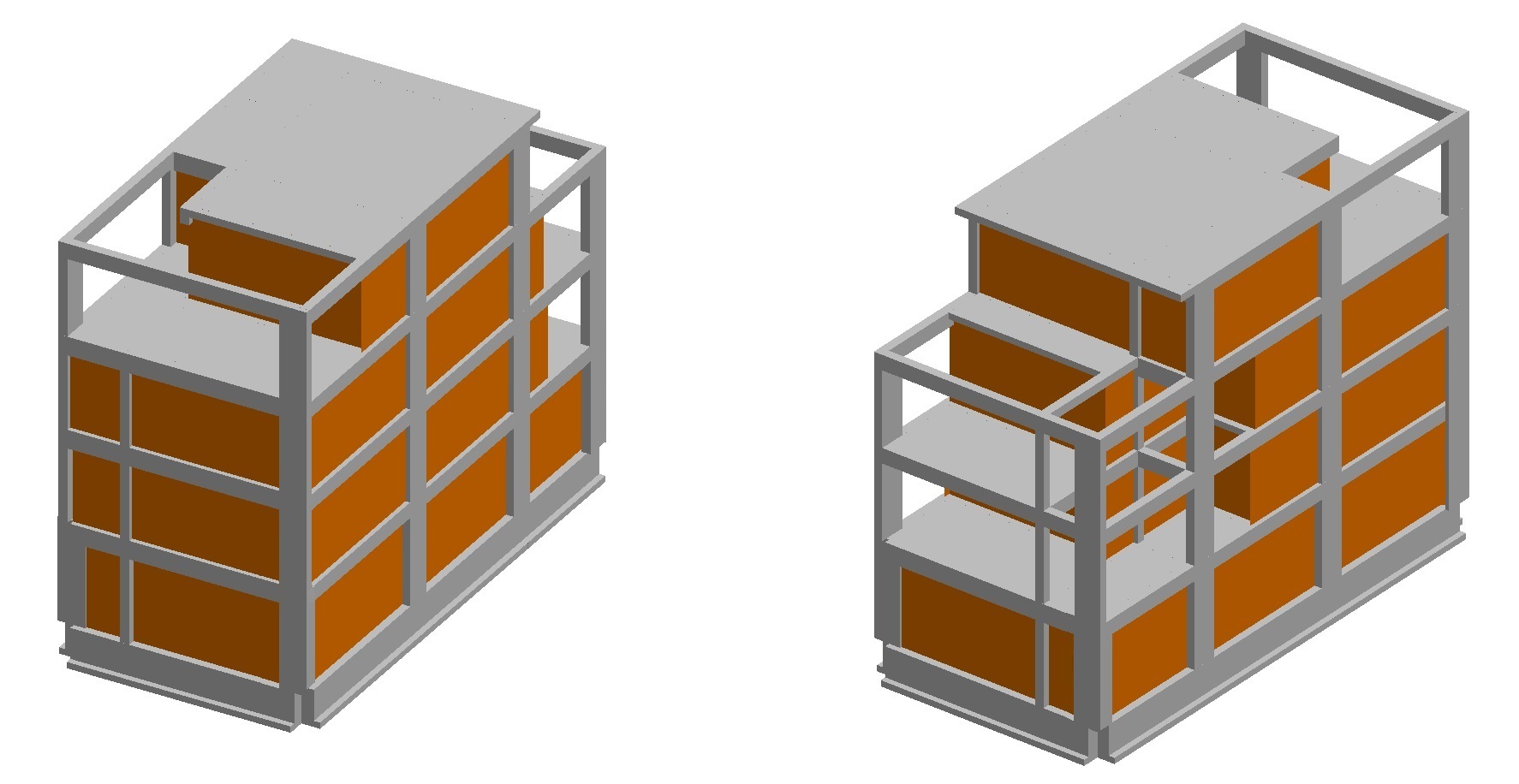
Figura 3: Vista tridimensionale del Corpo A
In definitiva, le principali problematiche di modellazione per il caso in esame sono:
– Modellazione dell’irregolarità delle tamponature
– Modellazione della rigidezza nel piano dei solai
Modellazione dell’irregolarità delle tamponature
Come possiamo notare dalle Figure 2 e 3, ad ogni livello sono presenti differenze distributive delle tamponature, sia per quanto riguarda la disposizione in pianta sia per la presenza e la distribuzione delle aperture.
Anche per il piano terra, che apparentemente presenta una figura rettangolare, la distribuzione delle aperture crea eccentricità nel posizionamento del baricentro delle rigidezze.
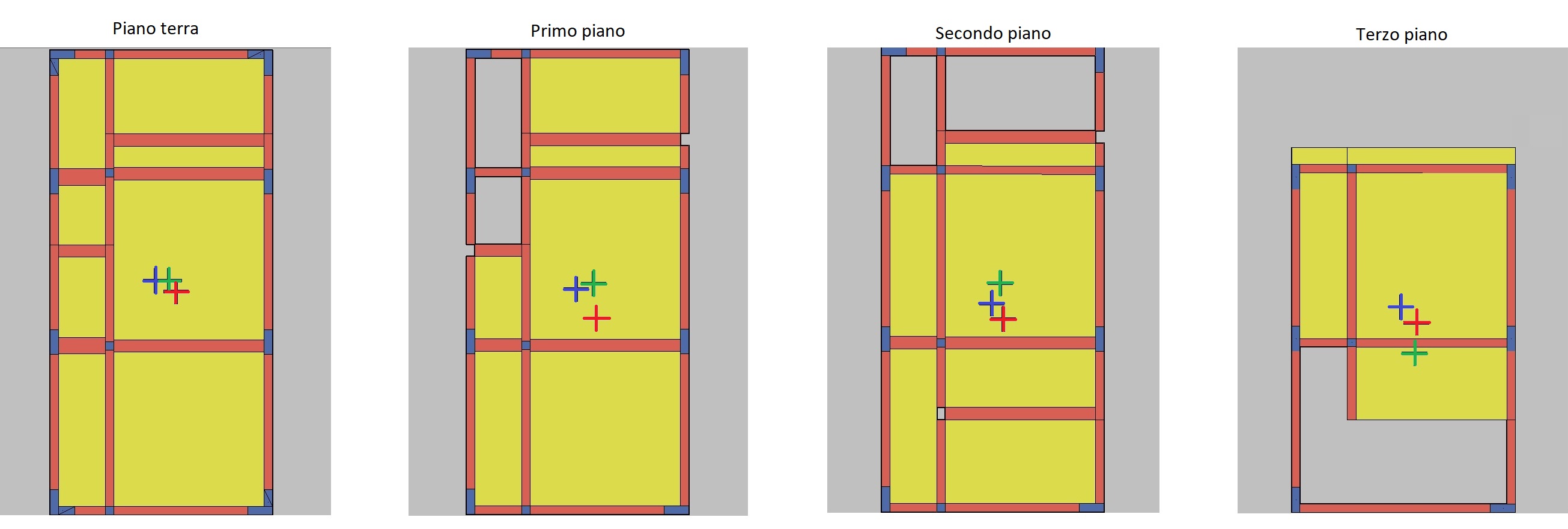
Figura 4: Baricentri di masse e rigidezze per i vari piani
Nella Figura 4 sono rappresentati i baricentri delle masse (in blu), delle rigidezze considerando le tamponature solo come massa (in verde) e delle rigidezze con la modellazione delle bielle delle tamponature (in rosso). Come possiamo notare (Figura 2) il piano terra è un unico ampio locale (destinazione d’uso commerciale) caratterizzato da vetrine ed accessi tutti dal solo lato sinistro della pianta, in quanto prospiciente alla strada. Questa situazione relativa a questi elementi non strutturali potrebbe creare squilibri nel comportamento sismico che è bene tener conto.
Per la modellazione delle tamponature utilizziamo un modello che consente di variare la rigidezza in funzione della quantità di aperture presenti. Un metodo molto semplice è quello presentato da Al-Chaar nel 2002. Il modello consiste nella schematizzazione di un telaio contenente dei puntoni equivalenti eccentrici che rappresentano la muratura.
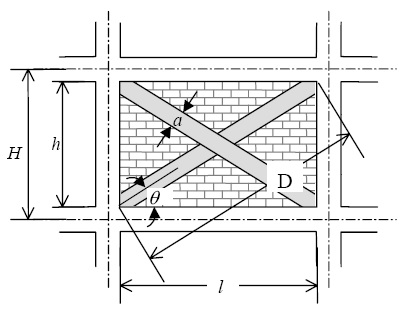
Figura 5: Bielle nel modello di Al-Chaar
La larghezza “a” del puntone dipende dalla rigidezza flessionale relativa telaio-pannello valutata con la seguente espressione (Stafford Smith & Carter – 1969):
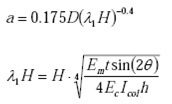
Figura 6: Formule relative al modello di Al Chaar
Oltre alle dimensioni geometriche, nelle formule sono presenti i comuni parametri che caratterizzano i pannelli murari, in aggiunta ai dati della maglia di struttura interessata:
t : spessore della muratura
Em : modulo elastico della muratura
Ec : modulo elastico dei pilastri in c.a.
Icol : momento di inerzia medio dei pilastri interessati
Per considerare le aperture e, nel caso di strutture esistenti, il danneggiamento è possibile ridurre il parametro “a” mediante i fattori R1 ed R2:
![]() Il fattore R1 è funzione del rapporto tra la superficie delle aperture e la superficie totale del pannello secondo la seguente espressione:
Il fattore R1 è funzione del rapporto tra la superficie delle aperture e la superficie totale del pannello secondo la seguente espressione:
 Nel caso in esame non consideriamo il danneggiamento e poniamo R2 pari ad 1.
Nel caso in esame non consideriamo il danneggiamento e poniamo R2 pari ad 1.
La presenza delle ampie aperture fa sì che di fatto il lato sinistro sia privo di elementi irrigidenti in quanto i vuoti sono superiori al 60% del totale. Per non scaricare troppo la struttura portante è bene considerare dei materiali delle tamponature non troppo performanti. Ad esempio per i blocchi di tamponamento la resistenza del blocco fbk è stato posto pari a 3 MPa e la malta dei ricorsi è di tipo M10.
Questa modellazione può essere ripetuta a tutti i piani, trascurando le parti di tamponatura non confinate da elementi in calcestruzzo. I risultati relativi alle posizioni dei baricentri delle rigidezze presentano, come è ovvio, delle differenze e sorprese (vedi Figura 4).
Per il piano terra, l’eccentricità massa-rigidezza aumenta per il modello con tamponature passando da 47.7 cm a 82.6 cm e presenta componenti anche nelle due direzioni.
Anche per il primo piano l’eccentricità per il modello con tamponature aumenta, raddoppiando da 66.1 a 127.6 cm.
Per il terzo impalcato le differenze sono tali da ribaltare la posizione del baricentro. In termini pratici vuol dire avere un comportamento di piano molto diverso in quanto si ha il “ribaltamento” tra “lato forte” e “lato debole”.
Per l’ultimo impalcato invece si ha una riduzione del valore dell’eccentricità passando da 173.2 a 79.2 cm.
Tutto questo ha, come è ovvio, ripercussioni nella distribuzione delle sollecitazioni e di conseguenza nelle armature, sia longitudinali che trasversali.
Modellazione dei solai
La forma dei vuoti (vedi Figura 4 – solai di colore giallo) suggerisce due possibili soluzioni al fine di modellare correttamente la distribuzione di rigidezza orizzontale attribuibile ai solai. I modelli sono:
– modello a rigidezza infinita (mediante legami master-slave)
– modello con elementi deformabili (mediante elementi finiti di tipo lastra)
Il primo tipo è quello storicamente più utilizzato in quanto, oltre che alla veridicità o meno dell’ipotesi di impalcato rigido, mediante questo modello vengono eliminati molti gradi di libertà del modello. Questa operazione consente, per ogni impalcato, di ridurre i gradi di libertà da 6n a 3n+6 (circa la metà), con n il numero dei nodi. Le relazioni tra i gradi di libertà dei nodi “slave” con il nodo “master” sono le seguenti (U spostamenti e R rotazioni):
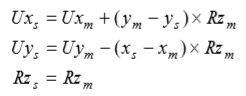 Oggi, grazie ai moderni computer questo non è più un problema, e quindi è possibile affrontare anche risoluzioni di modelli che consentono la “simulazione” di una rigidezza finita che, in rapporto con la rigidezza degli elementi verticali, consente di tener conto della deformabilità orizzontale dell’impalcato.
Oggi, grazie ai moderni computer questo non è più un problema, e quindi è possibile affrontare anche risoluzioni di modelli che consentono la “simulazione” di una rigidezza finita che, in rapporto con la rigidezza degli elementi verticali, consente di tener conto della deformabilità orizzontale dell’impalcato.
Nel caso in esame è stato utilizzato il secondo tipo di approccio in quanto, così facendo, si è riusciti a valutare lo stato di deformazione e le sollecitazioni sulle travi di bordo della parte forata, soggette anche ad azioni di flessione e taglio nel piano orizzontale. Nella Figura 7 è possibile notare la deformazione “non puramente traslazionale” della struttura, nonché l’accentuata deformazione delle travi dei fori nella direzione orizzontale.

Figura 7: Deformata dell’Impalcato 3 per Sisma X
L’elemento finito utilizzato è formulato per avere rigidezze solo per le componenti nel piano del solaio. A questi elementi si può attribuire un materiale di tipo “calcestruzzo”, quindi caratterizzato dal modulo elastico e dal coefficiente di Poisson, del tutto analogo a quello degli elementi strutturali. Lo spessore di queste “lastre” viene posto pari allo spessore della solettina del solaio (5 cm), trascurando l’anisotropia attribuibile all’orditura dei travetti (su questo ne parleremo in un altro articolo).
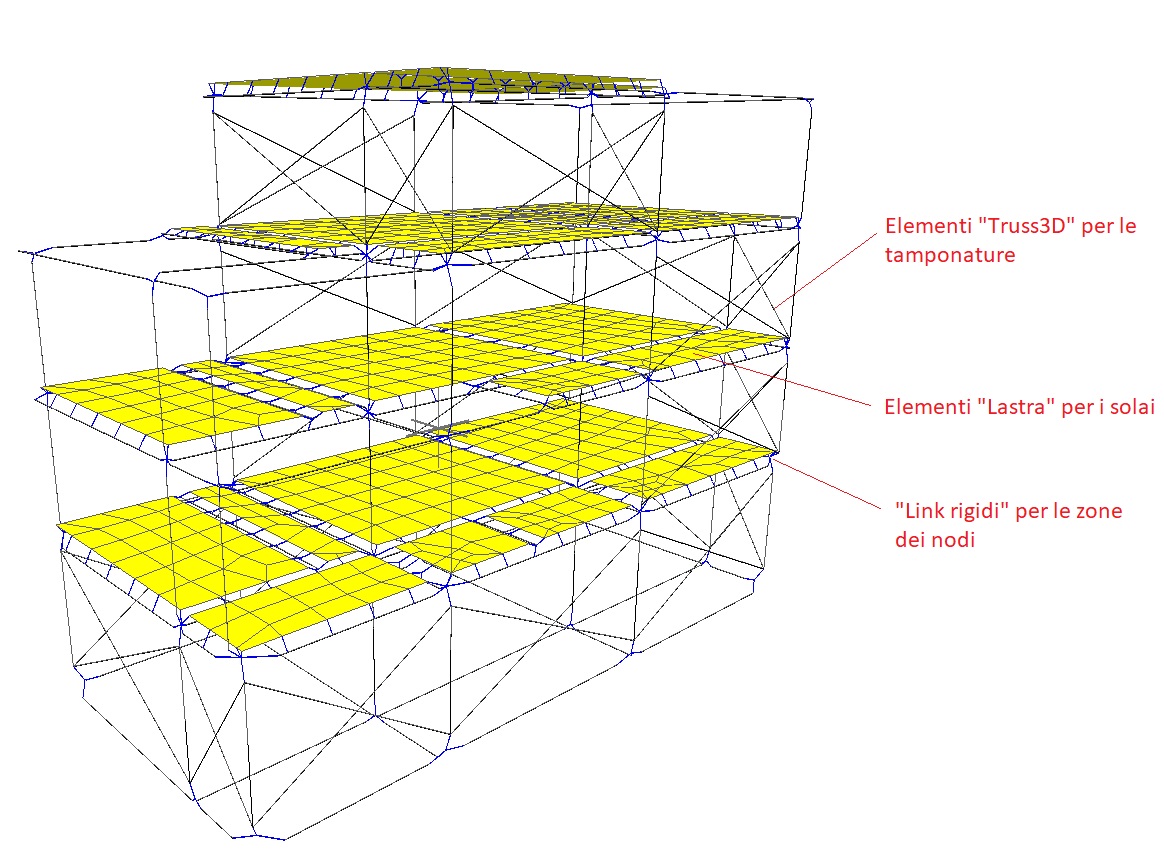
Figura 8: Modello FEM utilizzato
Per le travi di bordo della parte forata, considerando l’accumulo di sollecitazione causata dalla mancanza del solaio, si sono adottate armature di parete in modo da garantirne la “tenuta” in caso di evento sismico. Queste armature realizzano una vera e propria “armatura di pelle”, simile a quelle delle travi di collegamento di pareti dissipative. Se ci fate caso entrambi i casi collegano elementi di rigidezza molto più elevata delle travi stesse.
Soluzioni strutturali adottate
In definitiva, lo studio del modello finale (elaborato considerando la rigidezza delle tamponature e la deformabilità orizzontale dei solai) consente di applicare delle soluzioni tecniche che nella “pratica” intendono superare la “perversione teorica” dei modelli strutturali. Riassumendo abbiamo:
Aggiunta nuovi pilastri 30×30: Per tutta l’altezza dell’edificio è stata aggiunta una fila di pilastri di dimensioni 30×30 cm che hanno lo scopo di spezzare la luce delle travi (7.8 m) che gravano sul lato corto dei pilastri perimetrali. Così facendo si riduco le armature longitudinali delle travi con benefici sui nodi e sui pilastri adiacenti.

Figura 9: Ubicazione dei pilastri aggiuntivi 30×30
Struttura non dissipativa: Il basso valore dell’accelerazione di progetto SLV (0.14 g) ha suggerito la possibilità di progettare la struttura come “non dissipativa” con conseguenti vantaggi in termini di gerarchia delle resistenze e particolari costruttivi, soprattutto nei riguardi della duttilità.
Solaio alleggeriti tipo “Plastbau”: L’utilizzo di masse ridotte è sempre un vantaggio (differenza di 1.00 KN/m²). In modo particolare nel caso di strutture “non dissipative” ciò consente di limitare le sollecitazioni sismiche.
Pilastri ad “L” d’angolo del piano terra: Questi elementi hanno consentito di minimizzare gli effetti delle eccentricità dei baricentri dovuti alle irregolarità degli elementi non strutturali presenti. Inoltre, il carattere non dissipativo della struttura impone che le verifiche dei nodi vengano superate anche in presenza di elevati valori di sollecitazioni, soprattutto agli angoli. La scelta di utilizzo al solo piano terra è dovuta sia a vincoli architettonici, sia alle entità delle sollecitazioni.

Figura 10: Ubicazione dei pilastri ad L agli spigoli della costruzione
Armature trasversali infittite agli estremi (sia travi che pilastri): Anche se nel caso della progettazione “non dissipativa” è possibile seguire solo le prescrizioni del cap. 4 , ho preferito comunque infittire le staffe agli estremi degli elementi strutturali principali. Questo perché progettiamo il “prevedibile” ma dobbiamo anche essere pronti all'”imprevedibile”, e quindi ho voluto proteggere maggiormente gli elementi strutturali dal collasso fragile in caso di sisma. Così facendo il passo delle staffe è pari a 15 cm agli estremi e 20 nella zona centrale.
Armature di pelle per travi dei fori del solaio: Come già ampiamente spiegato in precedenza, queste armature sono necessarie per assorbire le deformazioni nel piano orizzontale provocate dal sisma delle travi che racchiudono le aperture nei solai, dovute alla mancata presenza del solaio in quel punto (vedi Figura 7 – travi con linea spessa nera).
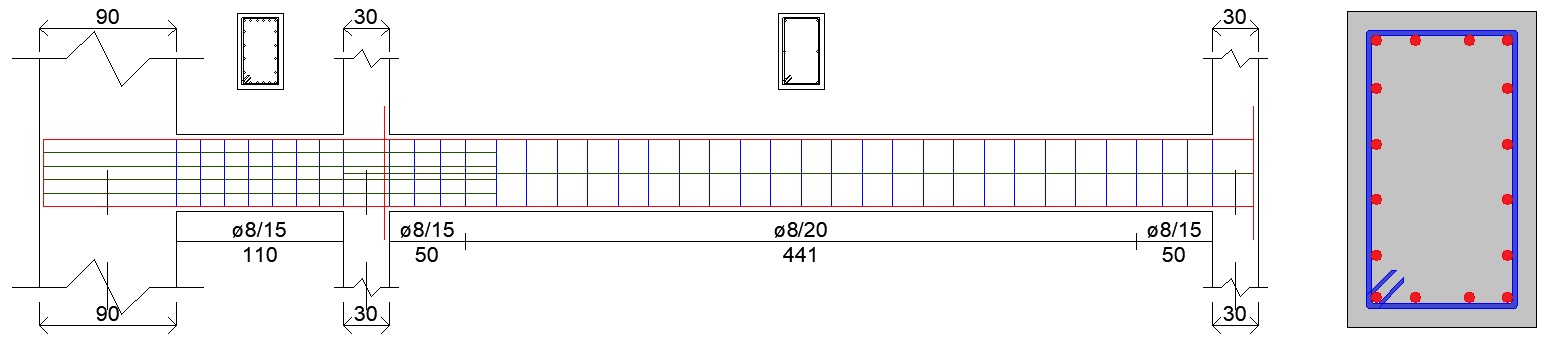
Figura 11: Armature delle travi per deformazioni orizzontali
Controllo della struttura con analisi statica non lineare
Come riportato in precedenza la struttura è stata progettata seguendo criteri di tipo “non dissipativo”, e cioè utilizzando un fattore di comportamento pari a 1.50 senza applicare le regole sui dettagli del capitolo 7 delle NTC 2018. Inoltre, per questo tipo di progettazione, le sezioni devono rimanere in capo elastico. Per garantire ciò le armature devono essere tali da non far superare la curvatura di snervamento della sezione. Questo tipo di approccio rappresenta per me un “piccolo ripiego” però, per avere il completo controllo del comportamento effettivo, ho elaborato, in fase di post-progettazione, delle analisi statiche non lineari per il calcolo del fattore di comportamento.
I risultati mi rincuorano. La disposizione di armature utilizzata, con l’aggiunta delle armature di rinforzo delle zone dei vuoti del solaio e l’opportuno raffittimento delle staffe agli estremi degli elementi, hanno portato ad un fattore di comportamento minimo delle varie curve pushover pari a 2.08. La struttura, pertanto, possiede delle caratteristiche di dissipazione che, per i bassi valori di accelerazione di progetto, possono soddisfare.
Progetto Architettonico : Arch. Rocco Cilurzo.


ottimo