 Il “tallone d’Achille” delle strutture soggette al sisma è la resistenza a taglio delle membrature e il conseguente collasso fragile. Un altro “tassello” del nostro puzzle per la definizione delle strutture antisismiche ci viene fornito dalla Circolare 7/2019 del CSLLPP.
Il “tallone d’Achille” delle strutture soggette al sisma è la resistenza a taglio delle membrature e il conseguente collasso fragile. Un altro “tassello” del nostro puzzle per la definizione delle strutture antisismiche ci viene fornito dalla Circolare 7/2019 del CSLLPP.
Spesso gli elementi strutturali in c.a. che presentano snervamento per flessione possono alla fine, sotto carico ciclico, collassare secondo modalità che mostrano chiari effetti tipici del collasso a taglio: evidenti crepe diagonali la cui loro larghezza ed estensione aumentano durante i cicli di carico. In tal modo i fenomeni di rottura associati alla flessione (fessure verticali nelle zone di massimo momento o instabilità delle barre) non hanno possibilità di manifestarsi nella maniera consueta.
La rottura a taglio sotto carico ciclico dopo il cedimento a flessione iniziale è definito collasso di “taglio duttile” (Kowalsky e Priestley 2000), e si può verificare anche con un solo carico ciclico, poiché la resistenza al taglio diminuisce più rapidamente con il ciclo di carico rispetto alla resistenza alla flessione.
Come ormai avete potuto constatare, la Circolare del CSLLP (così come le Norme Tecniche) non contiene nulla di inedito. La nuova formula indicata per la valutazione della resistenza a taglio è contenuta anche nell’ Eurocodice 8 ed è frutto di studi fatti dal ricercatore Dionysis Biskinis e dal prof. Michael Fardis, padre degli Eurocodici. La formula è la seguente:
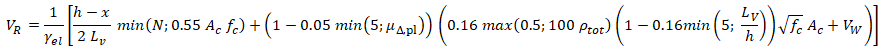 Il significato dei vari simboli è il seguente:
Il significato dei vari simboli è il seguente:
γel pari a 1.15 per gli elementi primari ed 1.0 per gli elementi secondari (come definiti al § 7.2.3 delle NTC);
h è l’altezza totale della sezione;
x è l’altezza della zona compressa della sezione (profondità dell’asse neutro);
N è lo sforzo normale di compressione (assunto pari a zero se di trazione);
LV è la luce di taglio;
Ac è l’area della sezione;
fc è la resistenza a compressione del calcestruzzo;
ρtot è la percentuale geometrica totale di armatura longitudinale;
Vw è il contributo dell’armatura trasversale per la resistenza a taglio.
μΔ,pl = θm-θy / θy = μθ – 1 è il rapporto tra la parte plastica della rotazione alla corda e la rotazione di snervamento
A cosa serve questa formula?
Questa diversa formulazione viene utilizzata per considerare la riduzione di resistenza alle azioni taglianti per il degrado dovuto a sollecitazioni cicliche (caratterizzate da continue inversioni). Queste inducono deformazioni cicliche inelastiche riferite alla fase di post-snervamento per flessione. Vediamo di essere più chiari…
Il funzionamento ottimale di una struttura antisismica richiede un’elevata duttilità, pertanto più l’elemento è duttile e più la sua “durata” sotto azioni cicliche è alta. Per garantire questa duttilità, in ogni caso, la rottura a taglio deve essere successiva a quella a flessione. In particolare, questa formula protegge dal collasso a taglio (definito dagli autori “taglio duttile”) dopo che sia già accaduto lo snervamento per flessione.
Nel caso di collasso a “taglio duttile”, la resistenza a taglio con le deformazioni cicliche anelastiche si riduce a tal punto da essere inferiore alla forza di taglio corrispondente al cedimento a flessione, Vy = My / Ls. La deformazione alla quale ciò avviene può essere considerata come la sua capacità di deformazione, governata dal taglio (vedi Figura 1). Riassumendo, come ulteriore prova dell’interazione tra i fenomeni, la resistenza a taglio è funzione anche del “livello di impegno” flessionale. All’aumentare delle deformazioni a flessione delle membrature diminuisce la loro resistenza a taglio.
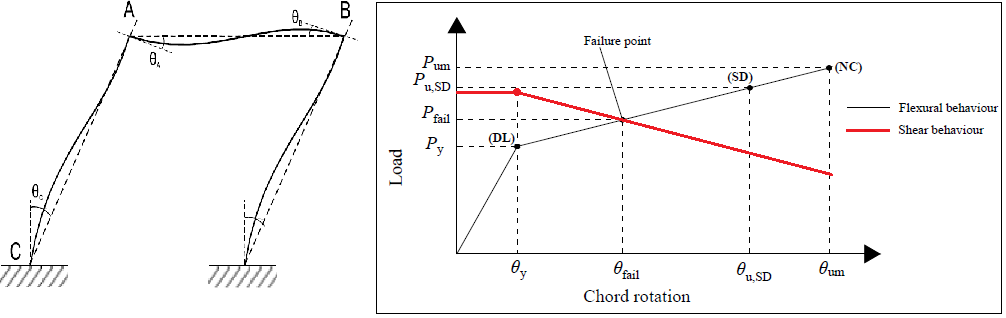
Figura 1 : Comportamento plastico degli elementi in c.a.
Nell’ambito dell’analisi non lineare l’utilizzo di questa formulazione consente di controllare il meccanismo “duttile limitato”. Nell’approccio classico della gerarchia delle resistenze (vedi Figura 2 (a) e (b)) il valore della resistenza è indipendente dalla rotazione alla corda. Nella Figura 2 (c) possiamo notare come anche nel caso del comportamento “duttile” è possibile che non venga raggiunta la rotazione ultima per flessione.

Figura 2 : Tipi di collasso – (a) Fragile – (b) Duttile – (c) Taglio duttile
Attendibilita dello studio.
I primi studi sul fenomeno sono stati elaborati da Kowalsky e Priestley 2000 sulla base di test di colonne circolari. Successivamente, nello studio di Moehle et al. (2001) il fenomeno è stato approfondito anche per pilastri a sezione rettangolare. Lo studio più importante in tal senso ha portato ai modelli elaborati da Biskinis et al. 2004, Biskinis e Fardis 2004, Biskinis 2007, e proposti nella parte 3 dell’Eurocodice 8 (CEN 2005a). Questi studi si basano sulla più grande banca dati dei test ciclici di elementi che collassano per tensione diagonale dopo la rottura a flessione. In particolare, oltre ad una prima fase di 239 test, sono state esaminate ulteriori 70 colonne circolari, 192 tra travi e colonne a sezione rettangolare, 12 pareti rettangolari e 26 pilastri rettangolari cavi o pareti composte.
Dal documento “Deformations of concrete members at yielding and ultimate under monotonic or cyclic loading” a firma Biskinis-Fardis si può notare come nei test eseguiti sia su travi, pilastri e pareti, ci sia un alto grado di attendibilità dei risultati ottenuti. Dai grafici seguenti si nota l’addensamento dei valori sulla diagonale, la quale corrisponde alla perfetta rispondenza tra valori predetti e riscontrati.
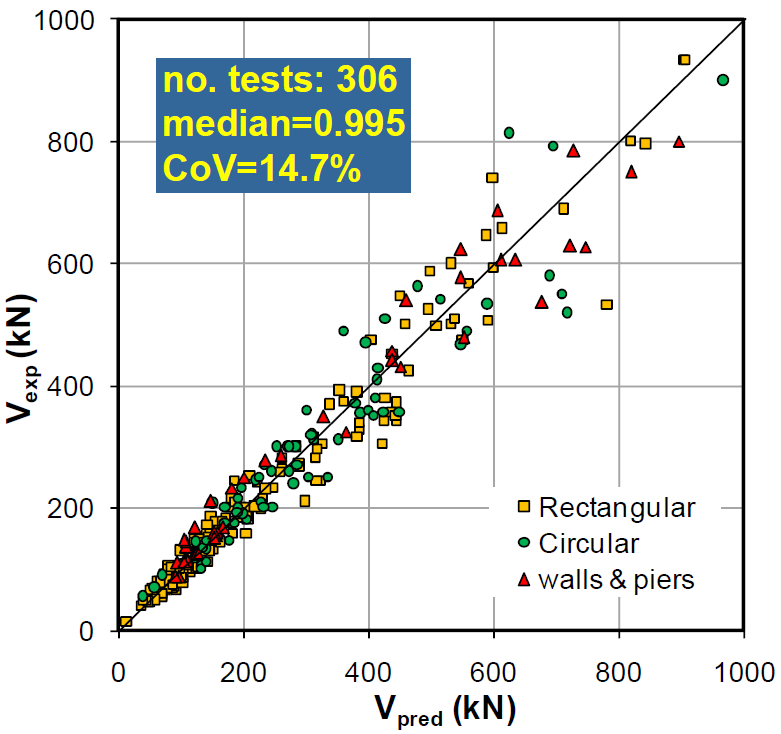
Figura 3 : Dispersione dei dati sperimentali rispetto alla formula
Il dimensionamento degli elementi in calcestruzzo contro la “rottura fragile” a taglio è un argomento oramai familiare, ampiamente trattato dagli attuali codici e standard per la progettazione di strutture in calcestruzzo sotto effetti delle azioni non sismiche che aumentano monotonicamente fino alla massima entità.
Quindi, sia per il progetto di nuovi edifici e la valutazione sismica di elementi esistenti il comportamento sotto sisma dovrebbe essere affrontato considerando anche la riduzione della resistenza al taglio sotto carico ciclico, che si manifesta al di sotto del valore massimo monotonico.
Commento ai contenuti della circolare.
Come avete ben capito l’argomento è molto importante. Purtroppo il testo della circolare non rende onore a tale importanza. Il primo refuso riguarda il coefficiente 0.5 utilizzato come limite superiore della duttilità plastica: sia nello studio di Biskinis-Fardis che nell’EC8 il valore corretto è 5.
 Un altro errore è il riferimento alla 8.7.2.7. È semplice verificare che il termine θu non è presente. Il riferimento corretto è 8.7.2.5. Inoltre, volendo essere pignoli (cosa che è divertente sul lavoro altrui), un’altra inesattezza riguarda la terminologia utilizzata per μΔ, che più correttamente dovrebbe essere μθ.
Un altro errore è il riferimento alla 8.7.2.7. È semplice verificare che il termine θu non è presente. Il riferimento corretto è 8.7.2.5. Inoltre, volendo essere pignoli (cosa che è divertente sul lavoro altrui), un’altra inesattezza riguarda la terminologia utilizzata per μΔ, che più correttamente dovrebbe essere μθ.
 Inoltre, a complicarne l’applicazione, nella Circolare 7/2019 sono presenti indicazioni volte a limitarne l’uso in funzione dello stato più o meno plastico dell’elemento. Anche se non riportati chiaramente è possibile distinguere quattro casi:
Inoltre, a complicarne l’applicazione, nella Circolare 7/2019 sono presenti indicazioni volte a limitarne l’uso in funzione dello stato più o meno plastico dell’elemento. Anche se non riportati chiaramente è possibile distinguere quattro casi:
- μθ < 1 : VR è pari al valore relativo al caso “senza staffe” (formula 4.1.23 NTC 2018);
- μθ < 2 : VR è pari al massimo valore tra il caso “con staffe” (formula 4.1.29 NTC 2018) e il taglio con riduzione ciclica (formula C8.7.2.8);
- 2 < μθ < 3 : VR si calcola mediante interpolazione lineare tra i valori di VR per μθ = 2 e μθ = 3;
- μθ > 3 : VR è pari al valore relativo alla presenza di riduzione per condizioni cicliche (§8.7.2.8).
A questo punto è opportuno ricordare che μΔ,pl = μθ – 1 in quanto i limiti indicati sono espressi per μθ e non in funzione di μΔ,pl . Per il caso μθ < 1 si deve inoltre controllare che l’elemento non sia in campo plastico. La Figura 4 contiene il diagrammi di flusso del calcolo di VR. Tutto questo lo trovate nel file xlsx, che potete scaricare in fondo alla pagina (e dall’area Download).
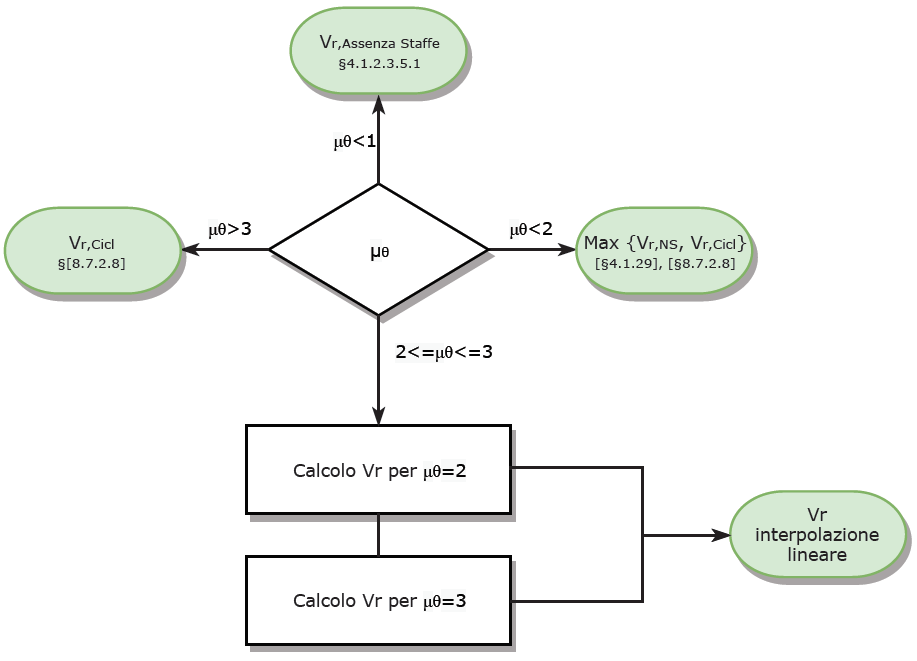
FIgura 4 : Diagramma di flusso per il calcolo di Vr
Osservazioni
Da sviluppatore di software, nell’implementare una nuova metodologia, è conveniente fare studi parametrici per capire quali sono i parametri più importanti entro valori plausibili. Elaborando diverse prove numeriche al variare di μθ possiamo notare che, rispetto allo sforzo normale N e alla luce di taglio Lv, la formula possiede scarsa sensibilità alla variazione della duttilità in rotazione. La correttezza del suo utilizzo è più che altro legato a tutta la formulazione stessa, in quanto risulta validata da numerose prove in condizioni cicliche. Al variare della duttilità μθ la variazione di valore di Vr è circa del 20%. Più alta risulta la sensibilità al variare dello sforzo normale (25 % circa), ed ancora più importante è la variabilità di Vr alla luce di taglio (circa 35%).

Figura 5 : Valori di Vr al variare di Lv, N, μθ
Come è possibile capire dall’utilizzo di formule approssimate sull’estensione della parte compressa la formulazione della resistenza a taglio in condizione cicliche è validata per flessione retta.
Metodo semplificato per strutture di nuova costruzione.
Secondo la circolare la riduzione della resistenza al taglio dovuta ad azioni cicliche è da applicare anche alle strutture di nuova costruzione. Applicando i concetti del “capacity design” diciamo che si segue già un criterio di sovraresistenza che tende a proteggere dal comportamento fragile. È anche vero però che il giusto funzionamento è basato su un valore di resistenza a taglio calcolato considerando i possibili fenomeni in gioco. In fase di progettazione si può aggiungere una semplificazione: partendo dal fattore di comportamento, mantenendo verificate le regole della gerarchia delle resistenze, si può imporre il valore massimo di duttilità plastica da raggiungere.
L’applicazione della formula per la valutazione del taglio resistente in condizioni cicliche è legata allo stato flessionale (attraverso la duttilità) e, pertanto, la verifica di resistenza è da effettuare per ogni singola combinazione. Questo per poter considerare i concomitanti valori di sforzo normale e momenti insieme agli sforzi di taglio. Come è semplice osservare, il problema si può risolvere in maniera rigorosa solo con l’ausilio di software appositamente programmati.
Volendo però stimarne il valore con semplici calcoli (come detto altre volte: “non siamo farmacisti”) possiamo, attraverso semplici passaggi, ricavare il valore “di progetto” di μΔ,pl dal fattore di comportamento q assegnato, in modo particolare se stiamo utilizzando analisi lineari. Partiamo de alcune definizioni:
- μδ : duttilità in termini di spostamenti
- μθ : duttilità in termini di rotazione alla corda
- μΦ : duttilità in termini di curvatura


Questo approccio è conservativo in quanto per la verifica di duttilità delle sezioni si è già obbligati a soddisfare le equazioni relative alla domanda di duttilità in curvatura.
Conclusioni.
Questa aggiunta contenuta nella circolare esplicativa alle norme tecniche vuole aggiungere un importante contributo alla progettazione delle strutture antisismiche. Come avete potuto constatare, questi concetti sono presenti da oltre dieci anni negli Eurocodici. Questo è accaduto ormai tante volte. Evidentemente la nostra comunità di studiosi o ci vuole far “ingerire” l’Eurocodice a pillole oppure non si fida completamente degli studi già presenti in letteratura. In ogni caso questo approccio rafforza ancor più il concetto di astrazione della progettazione in zona sismica. Le situazioni più gravose sono quelle che non si vedono…

