Effetti del second’ordine : approfondimenti per le strutture a telaio

Posted on by
Un modo semplice per considerare gli effetti della non linearità geometrica (effetti P-Δ) è, utilizzare la formula θ per impalcati suggerita sia dall’Eurocodice 8 (§ 4.4.2.2) sia dal DM 14/01/2008 (§7.3.1).
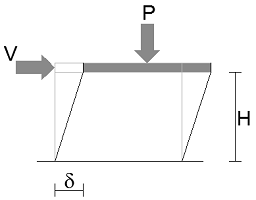
La formula è la seguentedove:
– P : rappresenta i carichi verticali agenti sulla testa delle colonne del piano considerato (per combinazioni sismiche G1+G2+Ψ2Q+E);
– δ : drift di piano (spostamento orizzontale relativo al piano considerato);
– V : tagliante totale agente al livello dell’impalcato del piano;
– H : altezza del piano.

 

Gli effetti del second’ordine sono tanto più gravosi quanto più la struttura è flessibile, in quanto a valori elevati degli spostamenti laterali corrispondono altrettanto elevati valori di momenti aggiuntivi (come nel caso di un evento sismico). Gli effetti dovuti a questo fenomeno, globalmente consistono in:
  1. Riduzione della rigidezza elastica laterale KE (il contributo di riduzione viene chiamato rigidezza geometrica KG);
  2. Riduzione della resistenza globale in termini di taglio alla base (V’y = Vy (1-θ))
  3. Riduzione della duttilità (pendenza negativa della fase post snervamento)
La formula proposta viene usata nel caso di analisi lineare e come vedremo è da utilizzare solo per edifici con impalcati rigidi. Questo limite sul campo di utilizzo è dovuto proprio alle ipotesi di base con le quali si perviene al rapporto (definito in letteratura “interstory drift sensitivity coefficient”). La formula nasce dal rapporto tra la rigidezza geometrica e la rigidezza elastica alle azioni orizzontali KG/KE:
Per l’ipotesi di impalcato rigido e per l’entità della deformabilità orizzontale la rigidezza elastica KE è calcolabile in modo semplificato come V/δ. La parte geometrica della rigidezza KG pari a -P/H è anch’essa frutto di semplificazioni in quanto si considera l’ipotesi che la deformata della colonna sia rigida, cioè dipenda solo dallo sforzo normale e dal drift di interpiano. In realtà, la matrice completa presenta mutue influenze tra i vari gradi di libertà. Come possiamo notare la formula di θ nasce dal rapporto KG / KE :

Una forma più generale del calcolo di θ è quella che utilizza algoritmi più generici basata sul rapporto P/Pcrit per ogni elemento strutturale. Il vantaggio operativo si ha maggiormente quando si utilizzano formule semplificate per il calcolo di Pcrit rispetto ad analisi di buckling, ma con le dovute approssimazioni. In questo caso il valore di θ va corretto moltiplicandolo per il fattore di comportamento q:

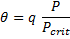L’alternativa di utilizzare l’analisi di buckling consente di superare i limiti di applicabilità del metodo in quanto si perviene a valori del moltiplicatore relativi a forme di instabilità elastica che consentono di prevedere le zone critiche da irrigidire.

 

Tornando alla formula di θ, in funzione del valore che presenta, si possono considerare quattro possibili casi:
  1. θ < 0.1 : gli effetti P-Δ si possono trascurare
  2. 0.1 ≤ θ ≤ 0.2 : gli effetti P-Δ si possono considerare moltiplicando gli effetti dell’azione sismica per 1/(1-θ)
  3. 0.2 < θ ≤ 0.3 : gli effetti  P-Δ devono essere valutati con metodi non lineari
  4. θ >0.3 : la struttura va progettata riconsiderandola in termini di rigidezza
Affrontiamo adesso un semplice esempio al fine di operare un confronto numerico tra i due metodi citati. Consideriamo una piccola struttura in acciaio con colonne HEA200 (orientate con la maggior rigidezza tutte nella stessa direzione) e travi IPE200. I solai sono realizzati in lamiera grecata con solettina in c.a. di 4 cm.
Le condizioni di applicabilità del coefficiente θ sono ampiamente rispettate. Per il piano terra, considerando un carico verticale P calcolato secondo la combinazione di carico G1+G2+Ψ2Q+E. otteniamo:
θ = P d / V H = 846.33 KN × 32.6 mm / 45.39 KN × 4000 mm = 0.152
Pertanto, per considerare gli effetti del second’ordine il coefficiente moltiplicativo da utilizzare pari a 1/1-θ è 1.18.

Effettuando l’analisi di Buckling per il calcolo del moltiplicatore di collasso, al carico verticale P precedentemente definito otteniamo un moltiplicatore minimo λmin pari a 17.06.

Il corrispondente valore di θ è pari a:
θ = q × P / Pcrit = 3.3 / 17.06  = 0.193
A tale valore corrisponde un moltiplicatore di 1.24.

Il confronto presentato è relativo a strutture definibili come “edifici” aventi impalcati rigidi e condizioni di regolarità. Come già accennato deve risultare chiaro che la formula semplificata θ non può essere estesa a tutti i tipi di strutture. In generale è preferibile utilizzare analisi di buckling, in quanto, implementate mediante il metodo degli elementi finiti, consentono di generalizzare forme e comportamento.

Gli effetti delle non linearità geometriche hanno un importanza rilevante in quanto hanno l’effetto di ridurre la resistenza alle azioni sismiche e la duttilità globale, con conseguente minori caratteristiche dissipative della struttura.

 

Bibliografia
Software utilizzati
File da scaricare:

2 thoughts on “Effetti del second’ordine : approfondimenti per le strutture a telaio”

  1. Buongiorno ingegnere, le volevo porre una domanda :
    su una copertura metallica spaziale (ralizzata con tubi e nodi sferici e pilastri circolari non controventata) ritrovo un coefficiete theta § 7.3.1 [7.3.1] di molto superiore (0,75) al limite di 0,3. Ora le NTC2018 prescrivono che in questo caso bisogna ridimensionare la struttura.
    Per prova ho ricavato con l’analisi di buckling alfa critico e quindi il theta (1/alfacritico) che invece risulta di circa 0,2.
    consultando glie eruocodici mi è sembrato di capire che la formulazione approssimata [7.3.1] è valida per stuttura a telaio trave-colonna (quindi non è il mio caso),
    La mia domanda è se posso fare riferimento al theta ritovato con l’analisi di buckling e verificare la struttura attraverso una analisi P-Delta, oppure, tenendo conto che il theta calcolato con formula [7.3.1] supera il limte di 0,3 la NTC mi impone comunque di riprogettare la struttura?
    Inoltre la formula [7.3.1] per tagli di piani prossimi allo zero fanno schizzare il theta.
    Grazie

    • Nel caso di una struttura reticolare sarebbe opportuno ricavare il carico critico dal moltiplicatore dell’analisi buckling. Il parametro teta è effettivamente più consono allo schema di funzionamento delle colonne. Il carico critico si può utilizzare direttamente nelle verifiche. E’ importante ricordare che se il moltiplicatore è inferiore a 10 andrebbero considerati gli effetti del secondo ordine (grandi spostamenti), vedi circolare 7/2019 §C4.2.3.4.
      Grazie per l’attenzione.

Lascia un commento