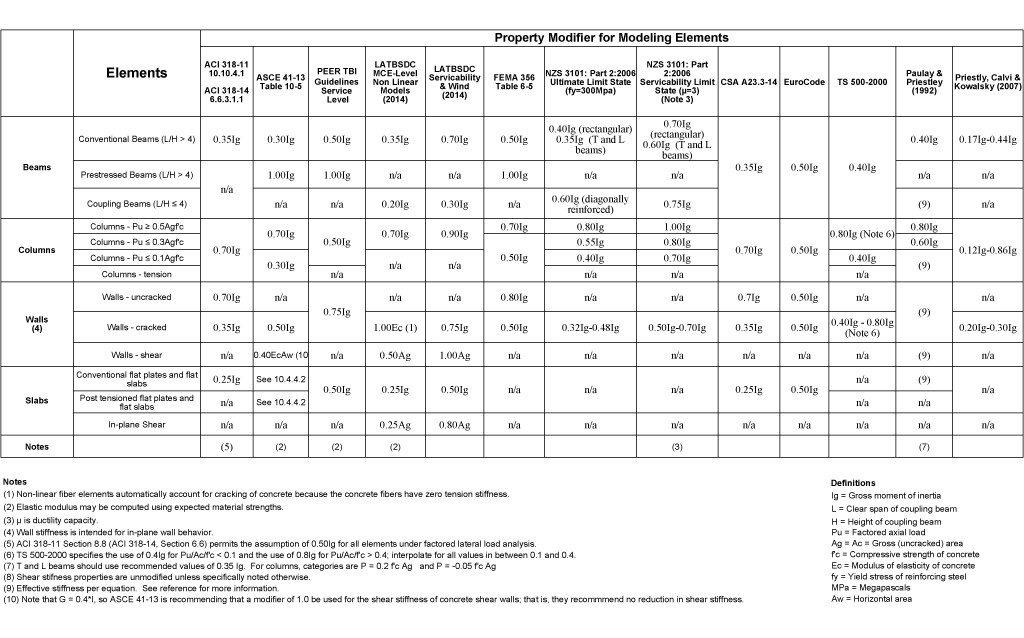
Le moderne procedure di progettazione strutturale sono basate sull’utilizzo del fattore di struttura (o di comportamento). Queste semplificazioni consentono di utilizzare forze laterali ridotte in modo da considerare un comportamento di tipo plastico sfruttando la semplicità applicativa delle analisi lineari elastiche. La rigidezza elastica da considerare (per elementi in calcestruzzo e muratura) dovrebbe essere coerente con il grado di plasticizzazione considerato in modo da considerare la condizione “fessurata”.
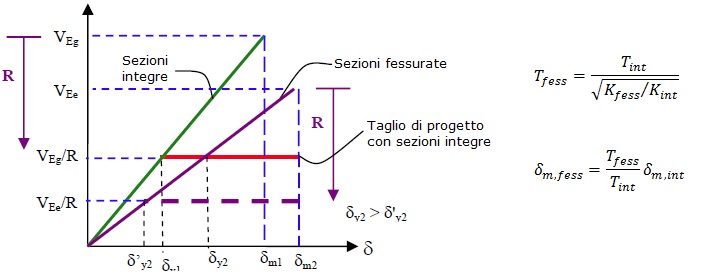
Fig. 1 : Effetti delle rigidezze fessurate nel comportamento dissipativo
L’errata modellazione della rigidezza può compromettere la stima del periodo di vibrazione fondamentale e il calcolo dei modi di vibrare, con conseguenti errate valutazioni delle sollecitazioni di progetto. Inoltre, nel caso di effetti P-D la rigidezza laterale riveste un’importanza fondamentale, in quanto la fessurazione comporta una notevole diminuzione di rigidezza e di conseguenza maggiore instabilità agli incrementi di carico assiale dovute all’azione sismica (ed es. moltiplicatore di buckling proporzionale alla rigidezza).
I vari codici normativi suggeriscono l’utilizzo, per gli elementi in calcestruzzo armato, delle rigidezze fessurate. Più precisamente ci si riferisce all’effettiva rigidezza dell’elemento allo snervamento incipiente. Come è verificabile dal confronto con analisi pushover, la rigidezza secante allo snervamento presenta valori molto bassi rispetto a quella elastica (da circa 0.2 a 0.5 volte di quella elastica – Figura 2).
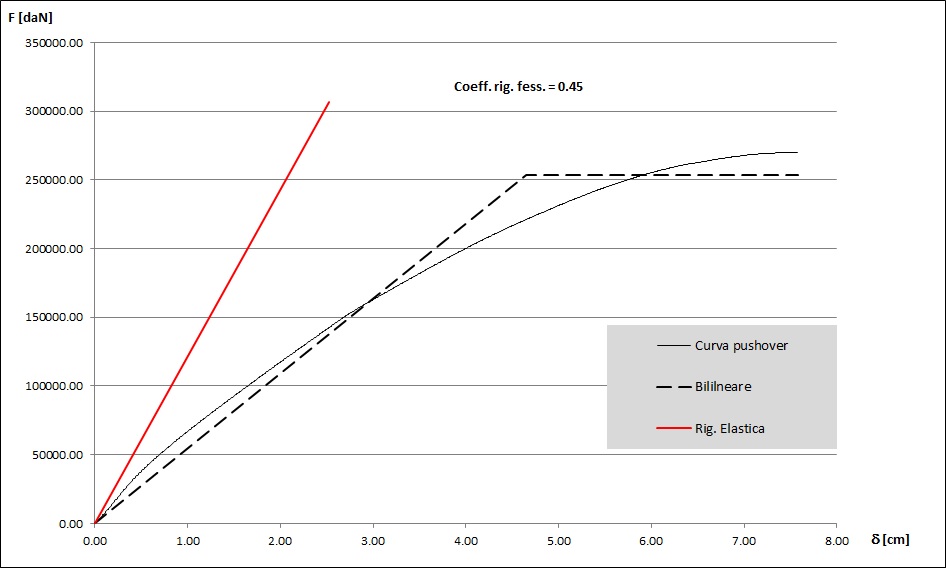
Fig. 2 : Esempio di valutazione del coefficiente di rigidezza effettiva
In realtà, la rigidezza in condizioni fessurate in un elemento strutturale dipende dai seguenti fattori:
- Stato di sollecitazione assiale
- Quantità di armature presenti
- Entità dei carichi laterali
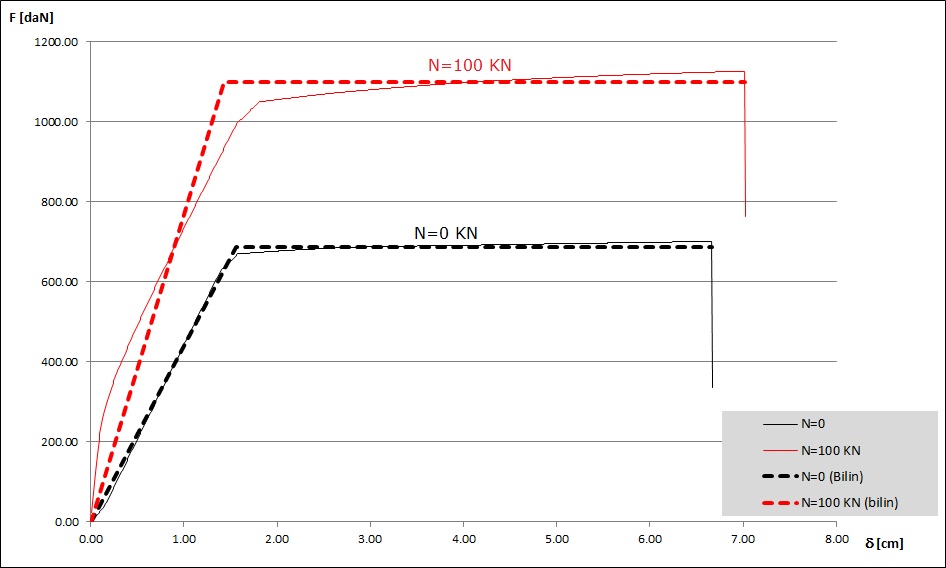
Fig. 3 : Effetti dello sforzo normale sulla rigidezza fessurata
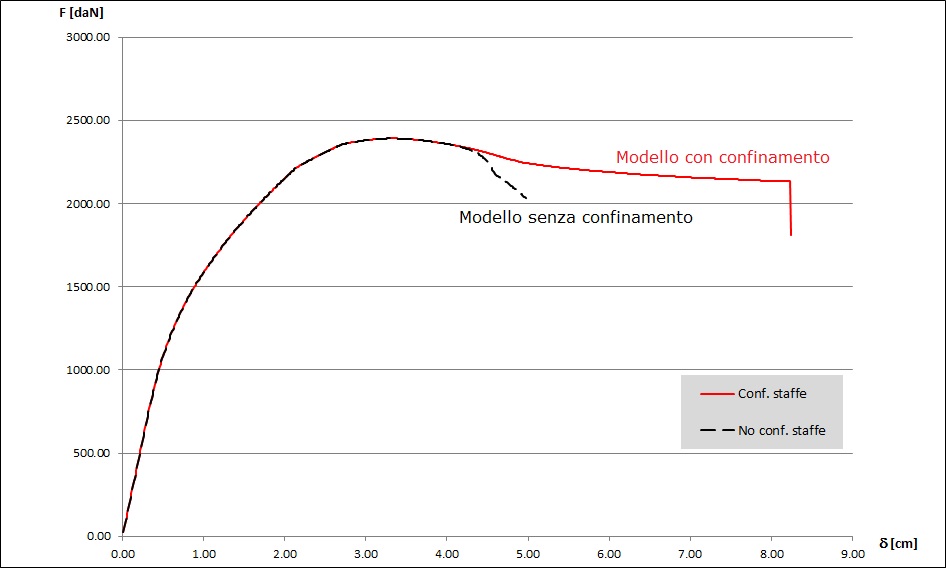
Fig. 4 : Effetti del confinamento mediante le armature trasversali. Modello di Kent & Park (1971) con indicazioni aggiunte da Scott (1982).
Per quanto riguarda i carichi laterali, la riflessione che si può fare riguarda il tipo di stato limite sismico da analizzare. L’entità degli spettri di progetto per SLV ed SLC comporta sicuramente stati di fessurazione elevata, mentre per gli SLD e SLO, essendo stati limiti elastici, la fessurazione non dovrebbe avvenire e pertanto è possibile utilizzare le rigidezze integre o, secondo alcune norme, “fessurazione debole”.
Fig. 5 : Tabella di confronto tra le varie indicazioni normative
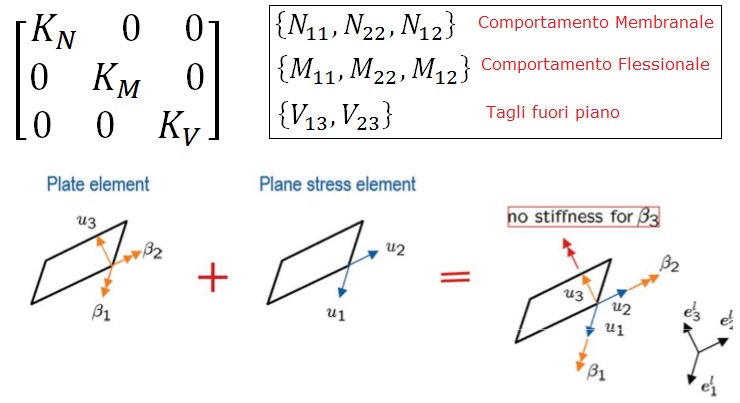
Fig. 6 : Matrice di rigidezza di un elemento shell e componenti di sollecitazione
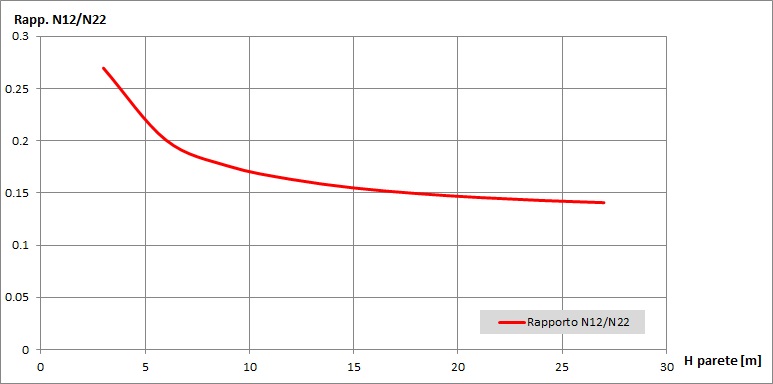
Fig. 7 : Rapporto tra N12 ed N22 al variare dell’altezza della parete
Fuori dal piano, nel caso non si utilizzi solo il comportamento membranale, le rigidezze fessurate devono essere utilizzate sia per la flessione che per il taglio. Per i solai modellati come piastre piene la rigidezza da variare è principalmente quella flessionale.
RIGIDEZZA FESSURATA PER L’AZIONE DELLA TEMPERATURA
Oltre all’ambito sismico, la rigidezza fessurata trova applicazione nel caso dell’analisi all’azione della temperatura. In questi caso il modello di calcolo dovrà essere differenziato in funzione degli stati limite analizzati. Per gli stati limite ultimi è possibile ridurre del 50% le rigidezze integre, per gli stati limite di esercizio il coefficiente di rigidezza può essere pari al 0.75.
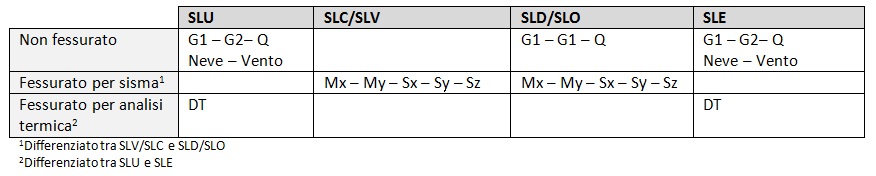
Fig. 8 : Modelli di calcolo da utilizzare in funzione delle azioni e dei vari stati limite
In definitiva, modelli di calcolo da utilizzare saranno i seguenti:
- Modello 1 – Modello a rigidezze non fessurate: Riguarda i carichi permanenti strutturali (G1), i carichi permanenti non strutturali (G2), i carichi d’esercizio (Q), le condizioni di carico statiche per Neve e Vento;
- Modello 2 – Modello con rigidezze ad elevata fessurazione: Riguarda le condizioni delle coppie torcenti accidentali di piano (Mx e My) e le condizioni sismiche nelle tre direzioni (Sx, Sy, Sz) per stati limite ultimi SLV e SLC;
- Modello 3 – Modello con rigidezze a bassa fessurazione: Riguarda le condizioni delle coppie torcenti accidentali di piano (Mx e My) e le condizioni sismiche nelle tre direzioni (Sx, Sy, Sz) per stati limite d’esercizio SLD e SLO;
- Modello 4 – Modello con rigidezze fessurate per DT: Riguarda l’azione termica per gli SLU;
- Modello 5 – Modello con rigidezze debolmente fessurate per DT: Riguarda l’azione termica per gli SLE.
In generale i modelli di calcolo da utilizzare sono 5, anche se comunemente, il Modello 3 e il Modello 1 possono assumersi coincidenti (ipotesi a sezioni integre), quindi i modelli di calcolo nelle condizioni più comuni diventano 4. In pratica però può essere utile raggruppare i modelli di calcolo in funzione dei valori dei coefficienti di fessurazione, in modo da diminuire al massimo il numero dei modelli diversi da implementare.
In conclusione, l’uso delle rigidezze fessurate è un modo immediato di realizzare un calcolo lineare ancor più affidabile e raffinato, senza perdere le sue caratteristiche di semplicità, e considerando, con le dovute approssimazioni, ulteriori fenomeni comunemente valutabili con analisi non lineari.
Bibliografia
FEMA 356 – Prestandard and commentary for the seismic rehabilitation of buildings
Computer modeling and effective stiffness of concrete wall buildings – M.IJ. Schotanus & J.R. Maffei