 Il “modulo di Winkler” o “costante di sottofondo” è il parametro più utilizzato (e più semplice da utilizzare) relativamente alla modellazione del contatto tra fondazione e terreno. Il modello al quale si fa riferimento ha origine nella publicazione sull’elasticità del 1867 di Emil Winkler, nella quale si affrontano varie problematiche strutturali.
Il “modulo di Winkler” o “costante di sottofondo” è il parametro più utilizzato (e più semplice da utilizzare) relativamente alla modellazione del contatto tra fondazione e terreno. Il modello al quale si fa riferimento ha origine nella publicazione sull’elasticità del 1867 di Emil Winkler, nella quale si affrontano varie problematiche strutturali.
Sin dalle prime applicazioni l’utilizzo di questo parametro è stato oggetto di confusione, sia per quanto riguarda la terminologia sia per i valori utilizzati. Nel 1955, Karl Terzaghi, nello studio “Evaluation of Coefficient of Subgrade Reaction, chiarisce che il valore del “coefficicente di reazione” non dipende esclusivamente dalla natura del terreno e fornisce dei criteri “correttivi” al calcolo del parametro elastico.
Nel modello di suolo elastico alla Winkler si ipotizza che la pressione esercitata dalla fondazione (intesa come elemento strutturale) sul suolo sia proporzionale all’abbassamento del suolo. L’espressione matematica che regola il modello è la seguente:
σ = K × w
dove:
σ : pressione agente sul suolo (in funzione del carico q)
K : costante di sottofondo (molle distribuite di rigidezza k)
w : spostamento verticale di un punto del terreno
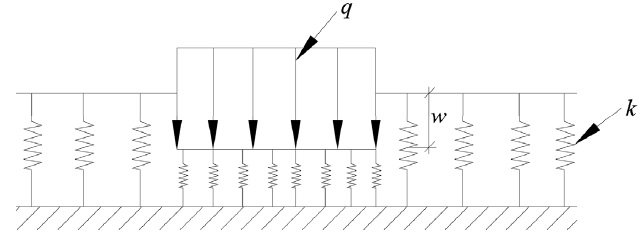
Figura 1: Modello alla Winkler
In realtà, come si può intuire, l’abbassamento del suolo dipende anche dalla rigidezza della struttura di fondazione. A parità di carico una fondazione rigida ripartisce più uniformemente sul suolo e quindi riduce la pressione applicata (e di conseguenza l’abbassamento). Viceversa, fondazioni basse comportano concentrazioni di pressione e quindi incrementi di cedimento del terreno.
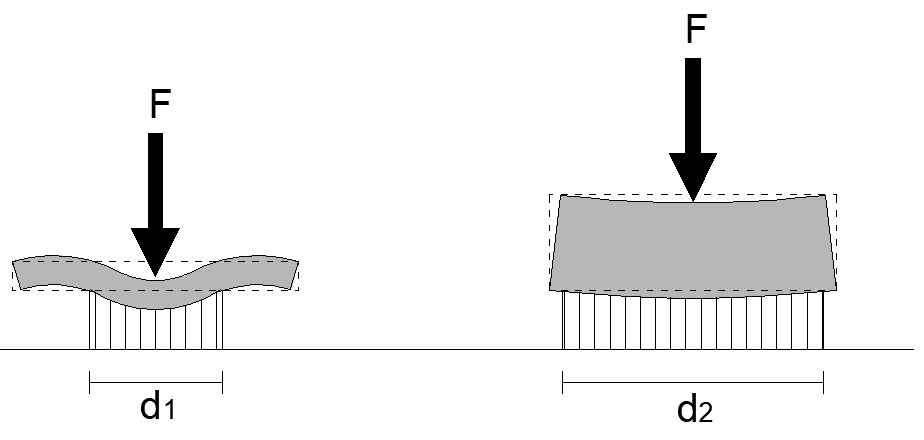
Figura 2: Influenza della rigidezza della fondazione
In maniera più completa, la reazione del sottofondo è funzione di:
- Proprietà elastiche del suolo (sia la risposta iniziale che la risposta a lungo termine dovuta al consolidamento del suolo
al carico prolungato); - Intensità del carico (che influenzerà il consolidamento a lungo termine);
- Dimensioni della superficie caricata e forma del carico su cui viene applicato (un’area di carico più ampia implica il consolidamento degli strati più profondi del suolo);
- Rigidezza della fondazione (che influenzerà la distribuzione della pressione sul suolo).
Tutt’ora in varie (e diffuse) pubblicazioni sono presenti tabelle indicative dei “Moduli di Winkler”, differenziati per varie nature del terreno di fondazione, che forniscono valori tali da “indurre in tentazione” il progettista ad usarli con leggerezza. E’ importante ricordare che è molto frequente che il valore della costante K non venga riportato nello studio stratigrafico del terreno di fondazione, vista la dipendenza dalla fondazione e la variabilità della scelta tipologica della fondazione stessa.
Semplici relazioni per calcolare la costante sono state studiate prima da Biot (1937) e poi integrate da Vesic (1961).

Figura 3: Formule per il coefficiente K
In questo modo, il valore del coefficiente K relativo alla direzione verticale viene calcolato utilizzando sia i dati geotecnici, sia considerando la rigidezza della fondazione. Le formule, che sono adatte per modellare l’interazione di travi di fondazione con il terreno considerato come mezzo elastico, sono elaborate a partire da:
Es : Modulo di deformazione del terreno;
vs : Modulo di Poisson del terreno;
Gs : Modulo di taglio del terreno;
B : base della fondazione;
E : Modulo elastico dell’elemento di fondazione;
I : Momento d’inerzia dell’elemento di fondazione;
Oltre ai limiti dovuti all’ipotesi sull’elasticità dei terreni, un’altra notevole approssimazione analitica è dovuta al fatto che secondo il modello alla Winkler l’abbassamento in una posizione non è influenzato dai punti circostanti: è come se la fondazione fosse adagiata su un “letto di molle” indipendenti l’un l’altra. Per queste motivazioni, il modello non consente di analizzare la mutua interferenza di due fondazioni indipendenti vicine.

Figura 4: Spostamenti verticali – a) Modello di Winkler – b) Spostamenti reali
Nonostante i limiti descritti è comunque un modello che ben si presta all’implementazione nel metodo agli elementi finiti, nel quale è possibile sia creare direttamente matrici di rigidezza con molle integrate, sia realizzare modelli discreti concentrando le molle ai nodi della mesh. L’utilizzo di rigidezze elastiche è stato esteso anche alle componenti orizzontali di vincolo della fondazione in modo da considerare anche la mancanza di un vincolo perfetto per il fenomeno dello slittamento (vedi Gazetas).
Problematiche legate alla modellazione
Come abbiamo introdotto in precedenza, il modello risulta essere vantaggioso nell’utilizzo del metodo FEM. In ogni aspetto della modellazione è bene essere consapevoli dei “tranelli” nel quale ci si può imbattere. Un primo esempio può essere il caso di un elemento uniformemente caricato.
In questo caso, l’indipendenza delle molle fa sì che ogni porzione di suolo risponda senza considerare le altre componenti di deformazione e rigidezza laterale. Il risultato è che la fondazione si abbasserà uniformemente della stessa quantità in ogni punto e la trave risulterà indeformata e quindi non sollecitata (M, N e T nulli in ogni punto).
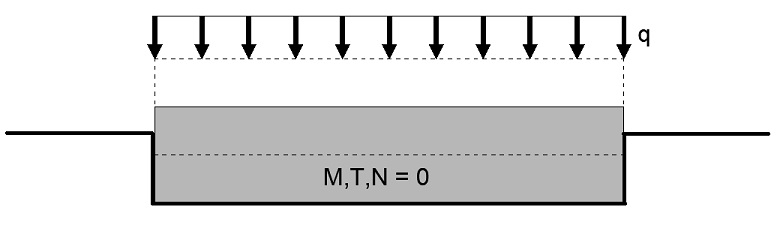
Figura 5: Sollecitazioni nulle con carico uniforme
Per risolvere questi problemi esistono modellazioni appositamente pensate, principalmente basate sul FEM, per ricreare un effetto più qualitativamente vicino alla realtà. I modelli più complicati sono assemblati partendo dal modello di Winkler utilizzando molle e strati con rigidezza a taglio o trazioni applicate. Tra questi, a scopo puramente informativo, citiamo il modello di Filanenko Borodich, di Hetenyi, di Pasternak e di Kerr (vedi Figura 6)
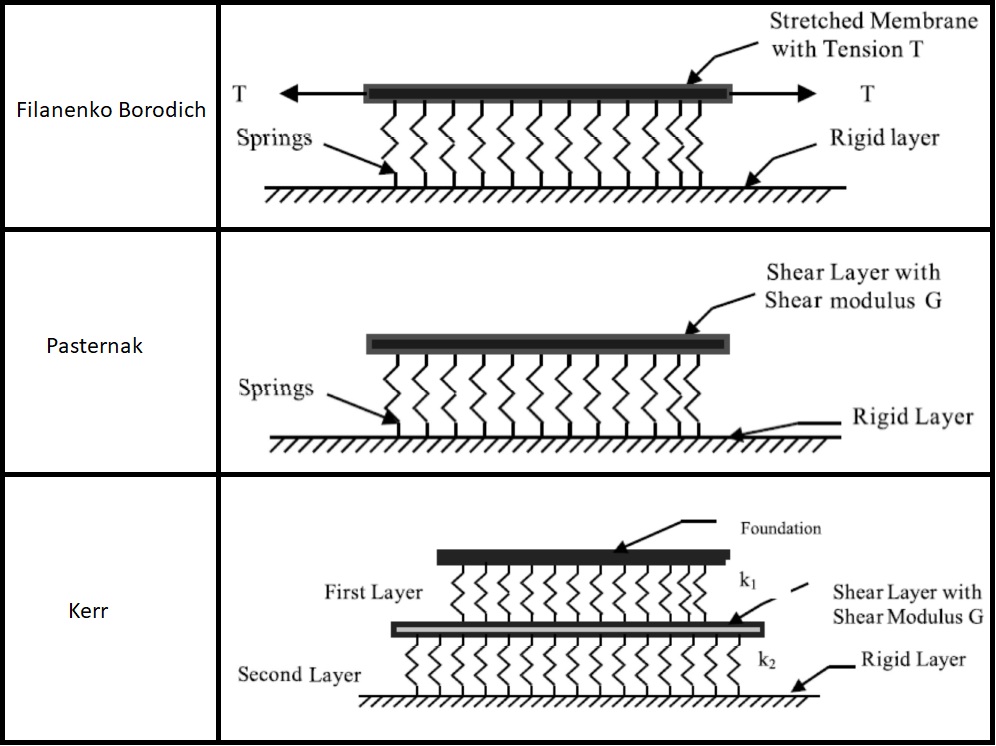
Figura 6: Esempi di modelli alternativi al Winkler
Un modello alternativo più semplice (e più utilizzabile nella pratica) è basato sulla “correzione” del modello di Winkler considerando che tale modello sottostima la rigidezza dei punti di estremità. Pertanto, in maniera molto semplice è possibile differenziare il valore delle rigidezze delle molle, incrementandolo dal centro verso le parti esterne (vedi Figura 7), cercando di calibrare il modello basandosi, per esempio, sulla teoria dell’elasticità.
Nell’esempio in figura, in presenza di una struttura di fondazione flessibile, è bastato applicare nelle zone dei bordi rigidezze pari a 4 volte il valore della costante K per ottenere valori soddisfacenti (vedi Figura 7-c).
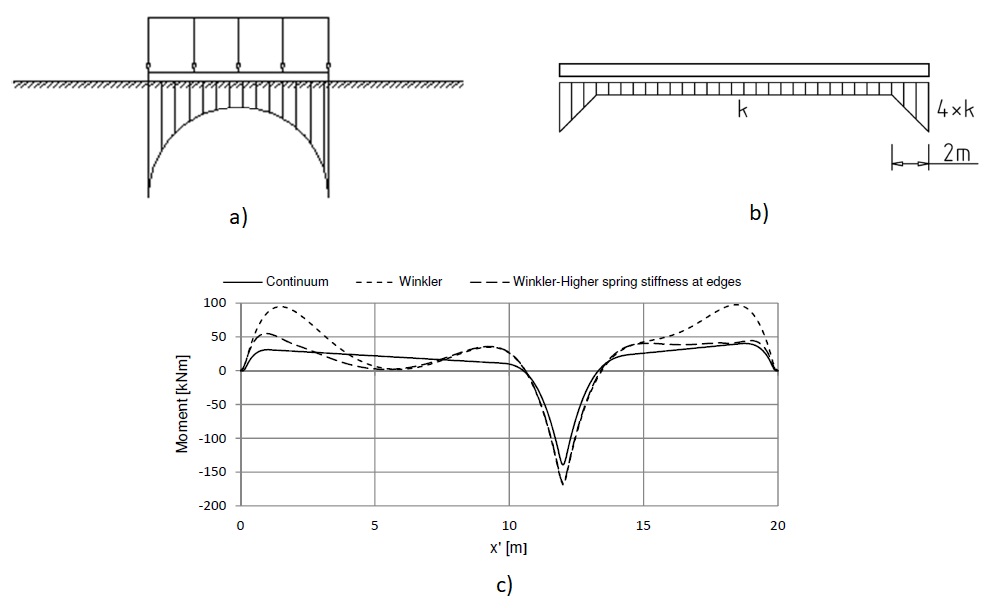
Figura 7: a) Pressioni con la teoria dell’elasticità – b) Modello di Winkler con rigidezze maggiori ai bordi – c) Confronto dei momenti alle varie ascisse
Nel caso di fondazioni di strutture a telaio la presenza delle rigidezze dei pilastri assolve tendenzialmente l’esigenza di concentrare ai punti perimetrali le rigidezze stesse (vedi Figura 8), anche se in maniera più o meno arbitraria. Su fondazioni isolate la taratura di questi modelli risulta complicata, soprattutto per quanto riguarda il fatto che dopo aver effettuato alcune prove di calcolo, ci si accorge che variando i parametri si entra in un “limbo” di incertezza caratterizzato da valori di sollecitazione dell’elemento di fondazione molto variabile.

Figura 8: Diagramma dei momenti a carichi verticali con il modello di Winkler per un telaio
Un altro problema tipico riguarda l’elaborazione delle analisi dinamiche di strutture modellate con la presenza della fondazione su molle. Questi casi contengono un altro “tranello” legato al rapporto di rigidezza verticale con quella orizzontale. L’approccio classico per la valutazione degli effetti del sisma sulla parte in elevazione suggerisce di bloccare il modello (almeno in direzione orizzontale) all’interfaccia tra gli elementi resistenti verticali e la fondazione stessa. Così facendo però, nel caso in cui utilizzassimo valori bassi della costante K di Winkler, rischieremmo di “condizionare” i modi di vibrare principali, trasformandoli principalmente in spostamenti nella direzione verticale (vedi figura 9).
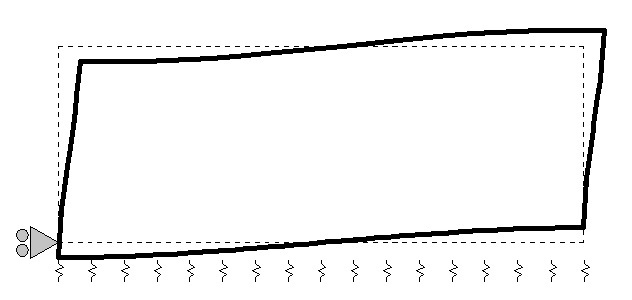
Figura 9: Modello con molle verticali e carrello orizzontale (1° modo)
Una possibile soluzione potrebbe essere applicare delle molle anche in direzione orizzontale. A tal proposito esiste un notevole numero di formulazioni elaborate da diversi studiosi, tra tutti ricordiamo le formule di Gazetas. Molto più grossolanamente (ma non meno efficacemente) possiamo provare ad utilizzare, come rapporto tra le rigidezze orizzontali e quelle verticali, la tangente dell’angolo di attrito tra fondazione e terreno (φ).
Facendo qualche calcolo da massaia (non me ne vogliano, è un modo di dire), con φ pari a 30° il rapporto è all’incirca 0.6. In tutto questo, non bisogna mai perdere di vista un altro problema. Se applichiamo rigidezze orizzontali molto basse rispetto alla struttura (vedi Figura 10) introduciamo un altro “condizionamento” ai modi di vibrare: è come se avessimo applicato degli isolatori sismici!
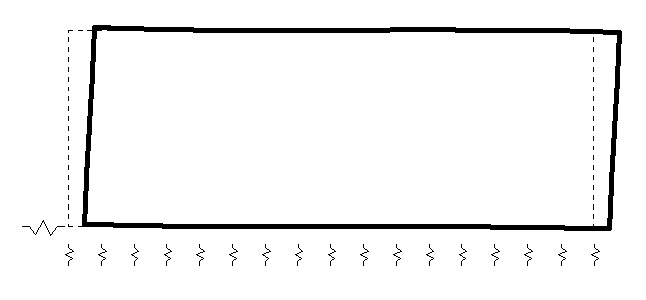
Figura 10: Modello con molle verticali ed orizzontali poco rigide (1° modo)
Come potete constatare nessuno dei due modelli che abbiamo visto sono ben calibrati. A questo proposito è bene fissare un concetto importante: i modelli di calcolo sono fortemente condizionati dalle rigidezze relative. Matrici di calcolo (soprattuto quelle delle rigidezze) in cui sono presenti alte differenze tra valori masimi e minimi potrebbero portare a soluzioni errate, come ad esempio la “labilità apparente”. In questi casi gli algoritmi di soluzione potrebbero esternare errori di labilità che in realta non si riscontrano applicando le classiche Scienze delle Costruzioni.
Conclusioni
Abbiamo visto come possa essere insidiosa la scelta del valore della costante di Winkler K alla luce dello studio del modello di calcolo più efficace da utilizzare. Come tanti aspetti del calcolo strutturale non bisogna mai perdere di vista ciò che differenzia un progettista da uno scienziato. L’obiettivo dei nostri modelli non è la realtà bensì la ricerca delle possibili conseguenze legate alla crisi degli elementi strutturali.
Per questo motivo probabilmente è bene non utilizzare un unico modello per tutto, ma diversificarlo in funzione delle finalità. Ricordo a tal proposito l’ottimo esempio dell’albero contenuto nel volume “Analisi modale ragionata” di P. Rugarli il cui significato è: se devo analizzare la sezione di base di un albero è inutile (e anche dannoso) modellare anche i piccoli rametti.
Ritornando alla costante K, sarebbe opportuno partire dai valori forniti dalle formule teoriche (Biot, Vesic, Gazetas, ecc.) e poi utilizzare diversi modelli per le diverse verifiche. Ad esempio, si può elaborare un modello (preferibilmente a base fissa) per valutare le sollecitazioni sismiche sugli elementi di elevazione, un’altro per valutare i cedimenti differenziali o la capacità portante della fondazione, ecc. Per fortuna, in modelli articolati e completi, la variabilità delle sollecitazioni sulle strutture di fondazione diminuisce all’aumentare della rigidezza delle stesse: le comuni dimensioni delle fondazioni sono già tali da darci una mano.
Spero di non aver seminato solo incertezze, ma credo che il dubbio renda le nostre scelte migliori.
Coming soon – Vi chiederete perché non vi ho ancora parlato della nuova Circolare sulle NTC 2018… L’argomento “tira”, ma ogni cosa va approfondita nel modo corretto (soprattutto le norme italiane!)… Datemi solo il tempo di “digerirla”…
Bibliografia:
Die Lehre von der Elastizität und Festigkeit – E. Winkler
Evaluation of subgrade reaction – K. Terzaghi
Beams on Elastic Subgrade and the Winkler’s Hypothesis – A. B. Vesic
Structural Element Approaches for Soil-Structure Interaction – A. Caselunghe, J. Eriksson

