Uno dei più importanti aggiornamenti pubblicati nelle nuove NTC 2018 è quello relativo all’utilizzo della domanda di resistenza valutata per il caso di comportamento strutturale non dissipativo come valore massimo per il criterio di progettazione in capacità. Questa indicazione consente di ottimizzare notevolmente la progettazione degli elementi tozzi e dei nodi strutturali. In questo articolo affronteremo, con semplici esempi pratici, l’applicazione di questa metodologia progettuale.
Riferimenti normativi
L’indicazione relativa all’utilizzo del limite sulla domanda è contenuta nel paragrafo 7.2.2 delle NTC 2018:
“…La domanda di resistenza valutata con i criteri della progettazione in capacità può essere assunta non superiore alla domanda di resistenza valutata per il caso di comportamento strutturale non dissipativo…”
In altre parole, nel caso di progettazione di strutture a comportamento dissipativo (q > 1.5) si può assumere come valore massimo della domanda quello che deriva dall’analisi della struttura come se fosse progettata con il comportamento non dissipativo (1 <= q <= 1.5). Ciò richiede quindi due analisi parallele in modo da avere disponibili le sollecitazioni per entrambi i tipi di comportamento.
Per poter approfondire adeguatamente l’applicazione pratica possiamo utilizzare due semplici esempi:
1. Calcolo della domanda per la verifica a taglio di elementi in c.a.
2. Verifica dei nodi travi-pilastro per strutture intelaiate in c.a.
Esempio 1: Calcolo della domanda per la verifica a taglio di elementi in c.a.
Ai fini della progettazione in capacità, per ciascuna direzione di applicazione del sisma la domanda a taglio VEd si ottiene imponendo l’equilibrio con i momenti (Mi,d) delle sezioni di estremità (superiore e inferiore) del pilastro, amplificati del fattore di sovraresistenza γRd, secondo l’espressione [7.4.5]:
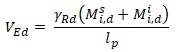
Formula E1.A
I momenti flettenti delle estremità si calcolano in funzione della capacità flessionale dell’elemento (momenti resistenti Mc,Rd della colonna), secondo la formula:
Formula E1.B
Nella formula precedente notiamo la presenza anche dei momenti resistenti delle travi (Mb,Rd) in modo da considerare una sorta di “gerarchia delle resistenze”, ovvero la capacità delle colonne è anche funzione della capacità delle travi (verifica a Presso-flessione §7.4.4.2.1). Da questa considerazione nasce un principio cardine della progettazione antisismica: la resistenza flessionale delle colonne deve essere sempre superiore alla resistenza delle travi.
Nell’esempio che faremo consideriamo una colonna di altezza (Lp) netta pari a 60 cm, in classe di duttilità B (γrd pari a 1.10), analizzando un solo verso e direzione del sisma. Il pilastro è relativo ad un impalcato intermedio e quindi ai suoi nodi convergono delle travi. Nell’esempio effettuato Le travi ai lati di ogni singolo nodo hanno una diversa capacità resistente a flessione.
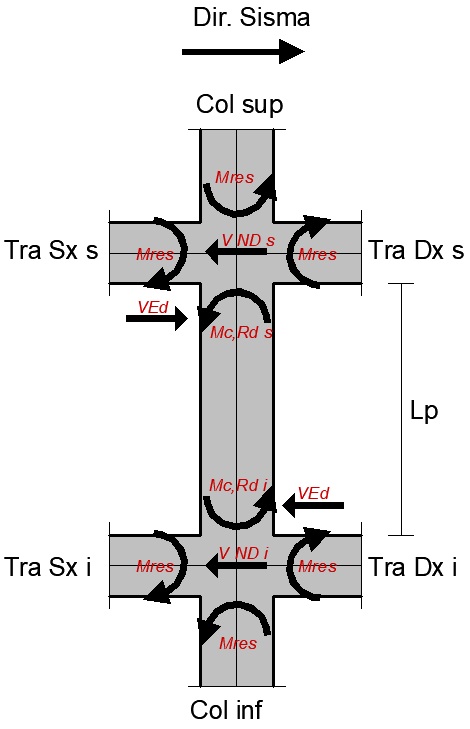
Figura 1: Dati per il calcolo della domanda a taglio
Iniziamo dal calcolo dei momenti Mi,d e di conseguenze della domanda VEd. L’applicazione della formula E1.A richiede che per ogni nodo vengano calcolate le seguenti grandezze:
Nodo superiore della colonna:
ΣMb = Mres Dx + Mres Sx = 104.5 + 61.1 = 165.6 KNm
ΣMc = Mres Sup + Mc,Rd s = 155.8 + 163 = 318.8 KNm
ΣMb/ΣMc = 165.6/318.8 = 0.52
Mi,d s = Mc,Rd s x ΣMb/ΣMc = 163 x 0.52 = 84.8 KNm (formula E1.B)
Nodo superiore della colonna:
ΣMb = Mres Dx + Mres Sx = 104.5 + 61.1 = 165.6 KNm
ΣMc = Mres Inf + Mc,Rd i = 168.9 + 164 = 332.9 KNm
ΣMb/ΣMc = 165.6/332.9 = 0.50
Mi,d i = Mc,Rd i x ΣMb/ΣMc = 164 x 0.50 = 82.0 KNm (formula E1.B)
Domanda a taglio:
VEd = γrd x (Mi,d s + Mi,d i) / Lp = 1.10 x (84.8 + 82.0) / 0.6 = 305.8 KN (formula E1.A)
Dall’analisi completa della struttura utilizzando il fattore di comportamento per strutture non dissipative (in questo caso q = 1.5) ricaviamo i valori del taglio sollecitante massimo sull’elemento in funzione delle combinazioni di carico in presenza di sisma (vedi §2.5.3 formula [2.5.5]):
Formula E1.C
Sollecitazioni a taglio con q=1.5:
Vsup = 109.5 KN
Vinf = 109.5 KN
Come possiamo notare il valore del taglio calcolato con la formulazione in capacità risulta molto più alto di quello al quale sarebbe soggetto l’elemento in condizioni già di per se molto gravose (valori dello spettro vicini a quello elastico). Progettare l’elemento a taglio potrebbe diventare proibitivo e non logico, pertanto si utilizza il valore Ved dato da:
VEd = min(305.8 , 109.5) = 109.5 KN
Esempio 2: Verifica dei nodi travi-pilastro per strutture intelaiate in c.a.
La domanda a taglio agente nel nucleo di calcestruzzo del nodo può essere calcolata in funzione della massima trazione trasferita dall’armatura longitudinale delle travi, secondo le seguenti formule (E2.A-1 per nodi interni e E2.A-2 per nodi esterni):
Formule E2.A-1 e E2.A-2
I parametri As1 ed As2 sono l’area dell’armatura superiore ed inferiore delle travi e Vc è la forza di taglio nel pilastro al di sopra del nodo, derivante dall’analisi in condizioni sismiche.
La verifica del nodo si basa su un meccanismo a traliccio che, a seguito della fessurazione diagonale, genera contemporaneamente un meccanismo di taglio-compressione e di taglio-trazione. I controlli da effettuare sono basati su entrambi i meccanismi. Per la verifica a taglio-compressione si deve controllare che nel puntone diagonale non si superi la resistenza a compressione del calcestruzzo, secondo la seguente relazione:
Formula E2.B
Per ulteriori approfondimenti e per il significato dei vari parametri si rimanda al §7.4.4.3.1. La verifica a taglio-trazione si ritiene soddisfatta disponendo nel nodo un’adeguata armatura di confinamento, progettata secondo le relazioni (la E2.C-1 per nodi interni e E2.C-2 per nodi esterni):
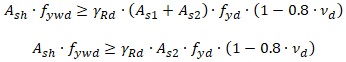
Formule E2.C-1 e E2.C-2
Il tipo di progettazione è “in capacità” in quanto le armature sono calcolate in funzione della massima trazione che può essere trasferita dalle travi. Nel caso in cui la trave fosse sovradimensionata, risulta chiaro che è necessario un limite nei valori di riferimento: questo limite può essere pari alla trazione indotta dalle sollecitazioni per comportamento non dissipativo. Con questa ipotesi la domanda relativa all’analisi “non dissipativa” con q<=1.5 può assumere i valori (la E2.D-1 per nodi interni e E2.D-2 per nodi esterni):
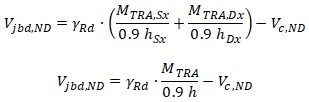
Formule E2.D-1 e E2.D-2
Nelle formule i valori MTRA rappresentano i momenti sollecitanti per comportamento non dissipativo relativi alle travi (pedice Sx per trave a sinistra del nodo e Dx a destra), le altezze h (per una o per le due travi) sono le “altezze utili” della sezione, e Vc,ND è il taglio agente sul pilastro al di sopra del nodo. Il termine 0.9 è relativo al calcolo della coppia interna agli stati limite ultimi. Il valore di Vjbd da utilizzare nella verifica a taglio-compressione è il minore tra quello delle formule E2.A e E2.D per i due diversi tipi di nodo.
Analogamente, per la verifica a taglio-trazione le formule diventano:
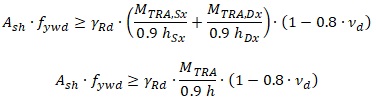
Formule E2.E-1 e E2.E-2
Affrontiamo adesso l’esempio numerico. Consideriamo un nodo d’angolo formato da un pilastro di sezione 300×600 mm e una trave concorrente di sezione 300×500 cm. La trave è armata sia superiormente che inferiormente con 4 Ø 14 di tipo B450C. Le staffe nel nodo (a due bracci) sono del diametro dell’8 al passo di 100 mm. I copriferri (intesi come distanza tra l’asse delle barre e la faccia esterna) sono tutti pari a 30 mm.
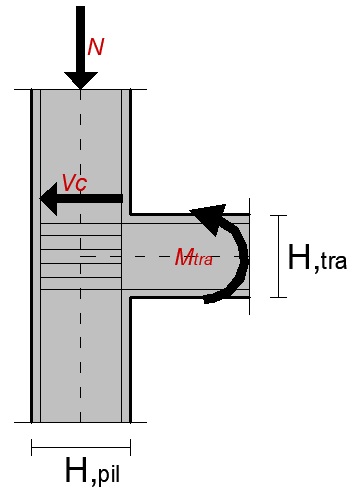
Figura 2: Dati per la verifica del Nodo
Sollecitazioni “Comportamento dissipativo”:
Vc,Diss = 19.7 KN
N,Diss = 55.5 KN
Sollecitazioni “Comportamento non dissipativo”:
Vc,ND = 49.2 KN
N,ND = 26.5 KN
Mtra,ND = 91.2 KNm
Verifica Taglio-Compressione:
Utilizzando la formula X e uniformando le unità di misura otteniamo il valore della domanda:
Vjbd,Diss = grd x As1 x fyd – Vc,Diss = 1.10 x 615.8 x 391 / 1000 – 19.7 = 245.14 KN
Vjbd,ND = grd x (Mtra/0.9 hTra) – Vc,ND = 1.10 x (91.2 / 0.9 / (500-30) / 1000) – 49.2 = 187.96 KN
Il valore da utilizzare sarà il minimo tra i due. In questo caso si utilizza il valore del comportamento non dissipativo, pari a 187.96 KN. Per la parte destra della disuguaglianza della formula E2.B abbiamo Vres,C = 1154.41 KN, ottenuto utilizzando i seguenti valori:
eta = 0.432
fcd = 16.7 MPa
bj = 300 mm
hjc = 540 mm
vd = 0.0088 (calcolato con N,ND per coerenza con la domanda utilizzata)
Vres,C = eta x fcd x bj x hjc x rad (1-vd/eta) = 0.432 x 16.7 x 300 x 540 x (1 – 0.0088 / 0.432) / 1000 = 1154.41 KN
L’esito di questa verifica è positivo in quanto Vres,C è maggiore di Vjbd (1154.41 > 187.96).
Verifica Taglio-Trazione:
Per questa verifica dobbiamo dividere le parti destra e sinistra della disuguaglianza della formula E2.E-2. Per la domanda (parte destra delle formule E2.C-2 e E2.E-2) abbiamo:
Val,Diss = grd x As2 x fyd x (1 – 0.8 x vd,Diss) = 1.10 x 615.8 x 391 x (1 – 0.8 x 0.0185) / 1000 = 260.92 KN
Val,ND = grd x (Mtra / 0.9 x h) x (1 – 0.8 x vd,ND) = 1.10 x (91.2 / 0.9 x 470 x 1000) x (1 – 0.8 x 0.0088) = 235.49 KN
Anche in questo caso si utilizza il valore del comportamento non dissipativo (in quanto è il minore), pari a 235.49 KN. Per la parte destra della disuguaglianza (formule E2.E-2) abbiamo Vres,T = 235.85 KN, ottenuto utilizzando i seguenti valori:
nbr = 2
HNodo = Htra = 500 mm
passo = 100 mm
As = pi x ز / 4 = 50.24 mm²
fyd = 391 MPa
Vres,T = nbr x ((HNodo / passo) + 1) * As * fyd = 235.85 KN
L’esito di questa verifica è positivo in quanto Vres,T è maggiore di min(Val,Diss, Val,ND) (235.85 > 235.49).
Dall’esperienza di questi semplici esempi possiamo notare che le nuove norme tecniche siano principalmente una revisione delle precedenti norme, volte ad una migliore applicazione e ad una progettazione più ottimizzata rispetto ai fondamenti base della progettazione in capacità. Il risultato finale sarà la realizzazione di strutture tecnicamente più semplici e con un livello di sicurezza immutato o addirittura superiore.
Note:
L’immagine in figura è una citazione della spiegazione sul “Capacity Design” dei Professori T. Paulay & M. J. N. Priestley.
Normativa:
DM 17/01/2018 – Norme Tecniche per le Costruzioni
File da scaricare:
Calcolo della domanda a taglio per pilastri - NTC 2018
Verifica dei nodi travi-pilastro in c.a. - NTC 2018
OTTIMO SITO, LO CONSIGLIERO’ AD AMICI
Tante grazie, spero di poter fare sempre meglio.
utilissimo un saluto
Grazie per la sua attenzione.
mi complimento per il sito che è riuscito a creare e, soprattutto a mantenere sempre aggiornato. Le chiedo, se una struttura è progettata nella modalità “non dissipativa”, la gerarchia delle resistenze si applica ugualmente?
Grazie per la sua attenzione. Nel caso di struttura non dissipativa la gerarchia delle resistenze non si applica in quanto l’utilizzo di q<=1.5 giustifica la mancanza dell'applicazione del capacity design.